DEVELOPPEMENT

• I) Les spectres lumineux
• II) Application de la spectroscopie à l'étude de la composition chimique et de la température du soleil
• III) L'effet Doppler-Fizeau

        Dans ce développement, nous répondrons à notre problématique :Quelles
informations peut-on obtenir de la lumière qu'un objet émet ?

I)Les Spectres lumineux

1)Les différents types de spectres

Spectre continu :
La lumière blanche est composé de toutes les couleurs du spectre : on dit que la lumière blanche possède un spectre continu car on passe d'une couleur à l'autre progressivement sans interruption. Tout corps solide ou tout corps gazeux sous forte pression, s'il est à
haute température donne naissance à un spectre continu

Spectre de raies d'émission
Certaines sources lumineuses n'émettent pas de spectre continu, ceci est le cas d'un gaz chaud et peu dense. En analysant la lumière émise par ce gaz à l'aide d'un prisme, on observe des raies brillantes : ce spectre est constitué de raies d'émission. Pour émettre
ce spectre, le gaz a absorbé de l'énergie. Il ne possède pas toutes les couleurs ; chaque élément chimique à l'état gazeux a son propre spectre de raies. Ceci nous amène à dire
que le spectre de raies d'émission d'un gaz est " son empreinte digitale ". La signature du
gaz est celle des atomes qui le constituent.

Spectre d'absorption
De même que les atomes peuvent rayonner de la lumière sous forme d'un spectre d'émission, ils peuvent aussi absorber de la lumière. Par exemple en faisant traverser par une lumière blanche un gaz froid, le spectre se trouve modifier : certaines couleurs ont disparu et l'on voit des raies noires, appelées raies d'absorption, les atomes ont absorbé sélectivement cette lumière. La propriété importante de ce spectre de raies d'absorption
est que ces raies se trouvent au même endroit que les raies d'émission.

Pour illustrer ces spectres, des expériences seront menées grâce à une fiche matériel demandé.

A l'aide d'une lampe crate, on éclaire à travers une fente puis une lentille pour obtenir une image nette sur un écran puis on intercale entre la lentille et l'écran un prisme ou un
prisme à vision directe. On observe ainsi un spectre continu :

En remplaçant la lampe crate par une lampe à vapeur de mercure on obtient un spectre d'émission :

En réinstallant la lampe crate et en intercalant une solution de permanganate de potassium entre la lentille et le prisme on obtient un spectre d'absorption :

Les lois de Kirchhoff
Les lois qui décrivent les conditions de formation de ces différents spectres portent le
nom du physicien Kirchhoff qui les publia en 1859 avec Bunsen :
Un gaz à pression élevée, un liquide ou un solide, s'il est chauffé, émet un rayonnement continu qui contient toutes les couleurs.
Un gaz chaud, à basse pression, émet un rayonnement uniquement pour certaines
couleurs bien spécifiques : le spectre de ce gaz présente des raies d'émission
Un gaz froid, à basse pression, s'il est entre l'observateur et une source de rayonnement continu, absorbe certaines couleurs, produisant ainsi un spectre de raies d'absorption.
Ce gaz absorbe les mêmes couleurs qu'il émettrait s'il était chaud.

On peut se demander comment se forme le spectre de raies

2) Formation du spectre de raies

La première condition pour qu'une raie spectrale, caractéristique d'un élément chimique, puisse se former est évidemment que cet élément chimique soit présent.
Ensuite lorsqu'un gaz est chauffé, l'élévation de température augmente l'agitation des
atomes qui se heurtent plus fréquemment et plus violemment. Lors de ces chocs,
l'énergie acquise se traduit par une perturbation du cortège électronique, les atomes recevant un supplément d'énergie qui les placent à un niveau d'énergie supérieur.

Ils sont excités, leurs électrons sont moins liés. Après le choc, l'atome se désexcite, les électrons " redescendent " à leur niveau d'origine, et l'atome retrouve son énergie initiale.
La différence d'énergie est libérée sous forme d'émission lumineuse, le photon. C'est une particule immatérielle et sans masse. Chaque photon d'un rayonnement (lumière, ondes radios, rayons X...) est porteur d'un quantum d'énergie caractéristique de sa fréquence (fréquence de la lumière = couleur).

Prenons l'exemple de l'hydrogène qui est l'atome le plus simple et le plus présent dans l'univers.
L'atome d'hydrogène peut absorber ou émettre des quantités (ou quantum) d'énergie
bien particulières : celles qui correspondent au passage de l'atome d'un niveau excité par une énergie En à un niveau plus bas, caractérisé par une énergie Ep inférieure à En se
fait avec émission de la différence d'énergie En-Ep.
L'atome peut émettre un photon dont l'énergie est égale à la différence d'énergie entre
les deux niveaux. Cette énergie correspond à une onde électromagnétique de fréquence
v ou de longueur d'onde l=c/l. Elle peut être déterminée selon la formule de Planck :
E=h.v ou E= h.c/l où :
-H est le facteur de proportionnalité et est appelé la constante de Planck. Il vaut aux alentours de 6,6260755xlO-34 (exprimée en J.S)
-E étant la quantité ou quantum d'énergie (en J)
-v la fréquence (en Hz)
-c étant la célérité (en m/s)
-l étant la longueur d'onde (en m)

L'atome peut aussi absorber de l'énergie, ceci lui permettant de passer d'un niveau
inférieur à un niveau supérieur, par exemple en absorbant un photon. Mais ceci n'est possible que si le photon possède exactement l'énergie nécessaire, c'est-à-dire la
différence d'énergie entre le niveau d'arrivée et le niveau de départ.

L'état stable d'un atome est son niveau d'énergie fondamental. Lorsqu'un atome est
porté dans un niveau excité, il n'y reste pas longtemps. Il revient à son niveau
fondamental en émettant un photon de longueur d'onde correspondante à la variation d'énergie de cette transition.

Série ; Première raie ; Limite ; Domaine
Lyman ; 0,1215 mm ; 0,0911 mm ; Ultraviolet
Balmer ; 0,6570 mm ; 0,3647 mm ; Visible
Paschen ; 1,875 mm ; 0,820 mm ; Infrarouge
Bracket ; 4,050 mm ; 1,458 mm ; Infrarouge
Pfund ; 7,409 mm ; 2,278 mm ; Infrarouge

3)Données obtenues à partir de l'analyse d'un spectre

Si l'on observe des raies caractéristiques d'un élément chimique dans le spectre d'un
corps, cela signifie qu'il y'a certainement cet élément chimique dans le corps. Lorsqu'un
gaz est formé de plusieurs éléments chimiques différents, le spectre est plus complexe.
On peut cependant identifier chacun de ces éléments si on connaît bien les spectres des différents éléments chimiques présents dans la nature. Lorsque que chaque raie a été identifiée, on a déterminé la composition chimique d'un gaz. Grâce à ce procédé, on
peut déterminer la composition chimique d'astres qui sont très éloignés.

La température d'une étoile dépend de l'étendue de son spectre. Prenons une lampe à incandescence :
Plus le courant électrique est grand, plus la lampe brille. Au début la lumière est rouge
puis va de plus en plus vers le bleu. Plus la température du filament augmente, plus le spectre d'étend et dévie vers le bleu. Ainsi on peut classer les étoiles selon leur
température de surface et leur couleur.

Il est possible de déterminer la proportion d'atomes occupant l'état d'énergie qui correspond au niveau de départ de la transition produisant cette raie et ainsi obtenir un deuxième indicateur de température. A mesure que la température croît, la proportion d'atomes excités au niveau n=2 par rapport au nombre total d'atomes et d'ions
commence d'abord par augmenter puis diminuer. L'intensité des raies de la série de
Balmer de l'hydrogène passe par un maximum pour une température voisine de 10000K. Cette intensité est donc un indicateur de la température qui règne dans le milieu où se
sont formées ces raies.
Pour déterminer l'abondance de l'élément, c'est très simple : pour une température
donnée, une raie est d'autant plus intense que l'élément chimique qui la caractérise est
plus abondant.

Ces études permettent de déterminer de nombreux renseignements sur les astres,
comme par exemple le Soleil

II) Application de la spectroscopie à l'étude de la composition chimique et de la température du soleil

Le spectre solaire peut s'obtenir simplement, en orientant un prisme ou un spectroscope, appareil à prisme ou à réseau permettant aussi de décomposer la lumière vers le ciel,
vers une région bien éclairée, à proximité du soleil. Cette observation nous permet
d'obtenir le spectre ci-après:
spectre solaire

On observe sur ce spectre des raies dites d'absorption, telles que nous en avons étudiées dans la partie précédente. Ces raies sont donc la signature des différents éléments
chimiques constitutifs du soleil. Parmi ces raies il y en a cependant certaines qui ne sont
pas dues à l'atmosphère solaire, mais à l'atmosphère terrestre. Tels que cette bande de l'oxygène, dans la partie rouge du spectre

Pour déterminer expérimentalement la composition de notre étoile, nous allons repérer
sur le spectre visible du soleil les quinze principales raies, et afin de connaître les
longueurs d'onde de ces raies nous allons y juxtaposer le spectre d'un élément chimique déjà étudié au préalable, ici, le spectre de l'argon, où nous avons marqué des valeurs des longueurs d'onde de ses raies caractéristique.

Nous avons le tableau ci-après.

Il ne reste alors qu'à comparer nos résultats avec les valeurs des longueurs d'onde l de différents éléments chimiques connues répertoriées dans le tableau ci-après.

De cette étude expérimentale, nous mettons en évidence que le soleil contient du Ca,
du H, du Fe, du Ti, et du Mg.

Les recherches scientifiques ont permis de connaître avec exactitude la composition chimique de notre étoile qui est récapitulée dans ce tableau :

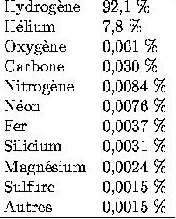
L'étude du spectre solaire permet aussi de déterminer la température du soleil en surface grâce à la loi de Wien, en effet, plus un objet est chaud, plus il émet de lumière dans les courtes longueurs d'onde. Ainsi, un métal peu chauffé émet dans le rouge. Il émet de
plus en plus vers le bleu quand sa température augmente, et finit par être perçue comme blanche. Ainsi, on a l'égalité suivante : lm*T=2900 mm*K
Le spectre continu de la lumière du soleil présente un maximum d'intensité lumineuse
dans le vert comme le montre la courbe ci-dessous :

Le maximum de luminescence se situe donc dans le vert aux environs de 480 nm. L'application de la loie de Wien donne environ T=6000 K.
La température de surface du soleil avoisine donc les 6000 Kelvins.

Le spectre lumineux peut enfin montrer la rotation du soleil, notamment par l'étude de
l'effet Doppler-Fizeau que nous allons maintenant aborder.

Haut de page

III) L'Effet Doppler-Fizeau

A) Présentation de l'Effet Doppler-Fizeau

1) Historique

C'est le physicien autrichien Christian DOPPLER qui expliqua en 1842 que notre perception de la hauteur d'un son est altérée par le mouvement relatif de la source sonore par rapport à l'observateur.
15 trompettistes furent placés dans un train et les expérimentateurs se placèrent au
bord de la voie. Quand le train arriva, les trompettes retentirent et la hauteur des sons
émis sembla diminuer quand le train fut passé, comme l'avait prédit la théorie de DOPPLER.
Il suggéra alors que les couleurs des étoiles pourraient être dues à un effet de ce type, affectant leur lumière. Mais en 1848, le physicien français Hippolyte. FIZEAU montra
que les vitesses des étoiles sont beaucoup trop faibles par rapport à la vitesse de la
lumière pour provoquer une modification appréciable de leurs couleurs. Il en conclut que l'on pouvait en revanche espérer détecter de faibles variations de longueurs d'ondes des raies dans leurs spectres. Cette conclusion fut vérifiée avec succès par l'astronome
anglais W. HUGGINS en 1868.

2) Vérification expérimentale

Nous savons qu'il existe une similitude entre la propagation des ondes sonores et électromagnétiques. Une modélisation de l'effet DOPPLER-FIZEAU pourra donc se restreindre à l'observation de la propagation d'ondes sonores.
Ainsi, cette modélisation consistera en la mise en rotation d'un buzzer ou d'une
quelconque source d'émission sonore constante.
Aussi, pour faciliter la compréhension du phénomène, il m'est possible de donner
l'exemple de " la voiture qui passe".

3) Explication du principe

En fait, cette altération de notre perception résulte de la compression et de la décompression des ondes, une conséquence du mouvement relatif de la source par
rapport à l'observateur.
-Quand une source se rapproche de l'observateur, il y a une compression des ondes ; la longueur d'ondes est plus courte.
-Par contre, quand une source s'éloigne d'un observateur, il y a une décompression des ondes ; la longueur d'ondes est plus longue.
Ce qui est vrai pour le son est vrai pour la lumière : le grave correspond au rouge, l'aigu
au bleu. En fait, cette variation de longueur d'ondes est une variation de périodes : la période d'une onde est la durée qui sépare deux passages successifs, par exemple de
son maximum, en un point fixe donné.
Si un observateur en mouvement cherche à mesurer cette durée, il lui trouve une valeur différente, plus élevée s'il se déplace dans le sens de l'onde, plus courte s'il se déplace en sens contraire. D'une manière générale, l'effet DOPPLER-FIZEAU modifie la période
d'un signal périodique.

B)Une source d'information majeure en astronomie

1)L'effet DOPPLER-FIZEAU en spectrohéliographie.

L'effet DOPPLER permet de mettre en évidence la rotation solaire par spectroscopie.
En effet, le soleil étant en rotation, le gaz au limbe est se dirige vers nous tandis que le
gaz au limbe ouest s'éloigne de nous.
Le principe de cette expérience consistait à prendre un spectre au limbe ouest et un
autre au limbe est pour mettre en évidence cet effet.
Ainsi, une dispersion suffisante du spectroscope doit donc nous permettre d'observer
un décalage des longueurs d'onde.

2)L'effet DOPPLER-FIZEAU en spectroscopie.

L'effet DOPPLER-FIZEAU joue un rôle très important en astrophysique car les astres
sont animés de vitesse les uns par rapport aux autres.
La vitesse est une notion essentiellement relative et quand on parle de mesurer la vitesse d'une étoile, il s'agit de la vitesse qu'elle a par rapport à l'observateur.
On utilise pour ce faire la propriété qu'a la lumière de changer de couleur suivant que la source lumineuse s'éloigne ou s'approche de l'observateur : bleue si elle a un mouvement d'approche, rouge si elle s'éloigne de nous.
Le spectre d'une étoile qui s'approche de l'observateur est décalé vers le bleu (vers les faibles longueurs d'onde), et celui d'une étoile qui a un mouvement de récession subit un décalage vers le rouge (vers les grandes longueurs d'onde "redshift").
Il est donc possible à partir de ce décalage de déduire la vitesse radicale des étoiles : la valeur de ce décalage est proportionnelle à la vitesse de l'étoile, plus précisément à la composante de sa vitesse qui traduit l'approche ou l'éloignement, que l'on nomme vitesse radicale.
Ainsi les astrophysiciens ont abouti à la relation suivante :
?v = Vr / c
?v= Décalage relatif de la longueur d'onde.
Vr= vitesse radicale de la source.
C= vitesse de la lumière.
Ce calcul montre que le décalage relatif de la longueur d'onde est proportionnel au
rapport de la vitesse de la source par rapport à l'observateur à la vitesse de la lumière.
Mais il est également possible d'en déduire des informations concernant l'agitation
thermique de la source émettrice.
En effet, la source de lumière est constituée de particules animées de vitesses différentes
les unes des autres ; l'effet DOPPLER-FIZEAU provoque un élargissement des raies spectrales observées. Les atomes sont animés de mouvements aléatoires dus à la température : Plus la température est élevée et plus ces mouvements sont importants,
donc plus l'éventail des longueurs d'onde observées est grand. La raie est donc d'autant
plus élargie que la température est plus élevée.

Le Soleil étant en rotation, le gaz au limbe Est se dirige vers nous tandis que le gaz au
limbe Ouest s'éloigne de nous. En prenant un spectre au limbe Ouest et un autre au limbe Est, on doit donc pouvoir observer un décalage des longueurs d'onde si la dispersion du spectroscope est suffisante.
Les spectres sont obtenus en positionnant successivement la fente du spectro aux limbes
Est et Ouest.
En valeurs arrondies, le soleil effectue une rotation en 25 jours à l'équateur, et un point de son équateur parcours 4.4 millions de km pendant cette durée. La vitesse à mesurer est donc de l'ordre de 2 km/s. Cette vitesse doit se traduire par un décalage Doppler de 589*2/300000 = 0.0039 nm pour la raie jaune du Sodium. Cela représente donc un
écart de 0.0078 nm entre les spectres Est (décalage vers le bleu) et Ouest (décalage
vers le rouge).

L'essai que j'ai réalisé donne une valeurs tout à fait comparable et confirme ainsi le bon fonctionnement de mon spectro.

La valeur mesurée du décalage entre les raies obtenues sur les bords Est et Ouest du
Soleil est effectivement d'environ 0,0075 nm. Remarquez les raies dues à l'atmosphère terrestre ( indiquées par "T") qui ne subissent pas ce décalage.

3)Une source d'information clef pour déduire l'évolution de l'univers.

La loi Hubble fut établie par l'astronome américain Edwin HUBBLE en 1929 en étudiant
un grand nombre de spectres de galaxies. Cette étude montra que la quasi-totalité des galaxies observées présentent des raies d'absorption décalées vers la partie rouge de leur spectre et par conséquent s'éloignent de la terre.
HUBBLE montra que la vitesse de récession des galaxies est d'autant plus importante qu'elles sont éloignées par rapport à nous.
Quelle que soit l'interprétation que l'on donne à cette loi, elle montre que l'univers évolue
et s'oppose à l'idée ancienne d'un univers statique.
La découverte d'Edwin HUBBLE, à savoir que l'ensemble des galaxies, c'est-à-dire l'univers entier est en expansion, bouleversa les théories cosmologiques de l'époque. Ce phénomène amenait tout de suite à se poser deux questions concernant d'une part, la création de l'univers et d'autre part son évolution.
L'analyse spectrale nous a donc permis de mettre en évidence l'évolution de l'univers, son expansion, constituant ainsi une preuve à la théorie du "big-bang".

Haut de page

Copyright@Skwi